树状数组 | 辞琼

写在最前

树状数组算是我目前学过最优雅好写的数据结构了。

树状数组也被称为二进制索引树(Binary Indexed Tree,BIT)，是一种高效的数据结构，它可以实现 $O(\log n)$ 的单点修改和前缀和查询。

当我们想实现单点修改和前缀和查询时，肯定会有人想到用一个数组来维护若干个小区间的和，使得修改和查询的复杂度都不会那么高。

树状数组便是巧妙的运用了二进制来实现这一想法。

现在我们存储每一个位置前面 lowbit 位的和，也就是是说 $c_i=\sum_{j=i-lowbit(i)+1}^ia[j]$ ，比如 $i=6$ ，那么我们可以先将 6 转化为二进制 $(0110)_2$ ，显然 $c[6]=a[5]+a[6]$ 。

这里偷借一下老师的图（（（（

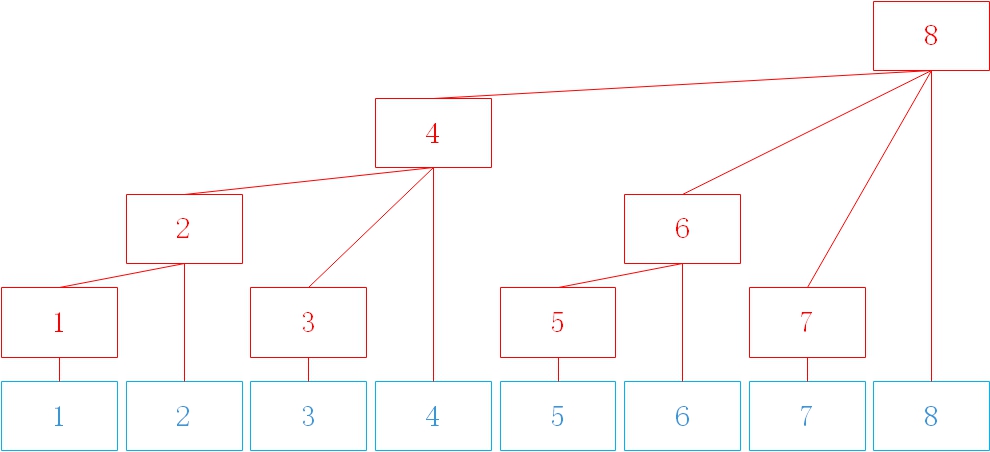
不难发现~~长得确实很像树~~如果现在要求前 $i$ 项的和，那么就可以通过每次减去 $lowbit(i)$ 得到的 $c_i$ 求和，具体来说就是 $sum[i]=c[i]+sum[i-lowbit[i]]$ 。

还是拿 6 举例，先化成二进制 $(0110)_2$ 。

所以 $c[6]=c[4]+c[2]$ 。

代码：

long long ask(long long x)
{
    long long sum=0;
    while(x)
    {
        sum+=c[x];
        x-=(x&-x);
    }
    return sum;
}

查询是从上往下退，修改也同理，从下往上爬就行了，不难发现， $i$ 的父节点即为 $i+lowbit(i)$ 。

代码：

void add(long long x,long long v)
{
    while(x<=n)
    {
        c[x]+=v;
        x+=(x&-x);
    }
}

“稍后”来写（（（（